Aula referente aos dias 15, 18 e 19 de junho de 2020.
Área do conhecimento: Matemática.
Objeto do conhecimento: Expressões Algébricas,
Monômios e Polinômios.
Professora: Adriana Alexandre.
O que é Monômio?
👉Um monômio, ou um termo algébrico, é uma expressão algébrica inteira composta por uma parte literal e um coeficiente numérico, isto é, por letras e números.
Por exemplo, 2x é um monômio, sendo que 2 é seu coeficiente e x é sua parte literal.
5ab2 é também um monômio, sendo que 5 é o coeficiente, e a parte literal é ab2.
👉Se dois ou mais monômios apresentam a mesma parte literal, trata-se de monômios semelhantes ou termos semelhantes.
Por exemplo, os monômios x, 2x e √3x são todos monômios semelhantes, pois todos apresentam a mesma parte literal x.
👉Entre monômios semelhantes, podemos efetuar a adição e a subtração como veremos a seguir:
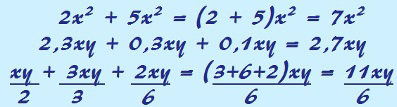
Ao realizarmos a adição de monômios, devemos somar os coeficientes e repetir a parte literal.
Para realizá-las, basta somar os coeficientes e repetir a parte literal.
👉 Caso os monômios em questão não sejam semelhantes, não há soma.
Por exemplo, a soma de 2x e 3y resulta simplesmente em 2x + 3y, um binômio, pois há a adição de dois monômios que não são semelhantes.
👉Se somarmos três monômios que não são semelhantes, teremos a formação de um trinômio.
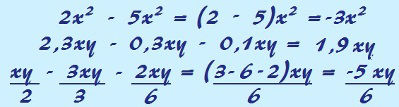
Para subtrair monômios semelhantes, nós subtraímos os coeficientes e repetimos a parte literal
👉Para realizar a multiplicação, divisão e potenciação de monômios, não é necessário que eles sejam semelhantes.
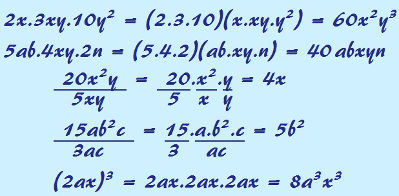
Para realizar as operações de multiplicação, divisão e potenciação de monômios, não é necessário que os monômios sejam semelhantes
VAMOS TREINAR!
"Copie e responda no caderno"
👉Calcule as adições e subtrações dos monômios:
Adição e subtraçãoEliminam-se os parênteses e reduzem-se os termos semelhantes.
a) 2x + 3x =
b) 6y – 4y + 5y =
c) 3a – 6a – a =
d) 7b + 4b – 6b =
e) 8xy – 4xy + 4xy – 8xy =
f) -3p -7p + 18p =
O produto de dois monômios, basta multiplicarmos coeficiente com coeficiente e parte literal com parte literal. E quanto multiplicamos as partes literais devemos usar a propriedade da potencia que diz para conservar a base e somar os expoentes.
b) 6y – 4y + 5y =
c) 3a – 6a – a =
d) 7b + 4b – 6b =
e) 8xy – 4xy + 4xy – 8xy =
f) -3p -7p + 18p =
👉Resolva as multiplicações com monômios:
MULTIPLICAÇÃOO produto de dois monômios, basta multiplicarmos coeficiente com coeficiente e parte literal com parte literal. E quanto multiplicamos as partes literais devemos usar a propriedade da potencia que diz para conservar a base e somar os expoentes.
a) (+5x) . (-4x²) =
b) (-2x) . (+3x) =
c) (+5x) . (+4x) =
d) (-n) . (+ 6n) =
e) (-6x²) . (+3x²) =
f) (-2y) . (5y) =
g) (+4x²) . (+5x³) =
h) (2y) . (-7x) =
i) (-2x) . (-3y) =
j) (+3x) . (-5y) =
k) (-3xy) . (-2x) =
b) (-2x) . (+3x) =
c) (+5x) . (+4x) =
d) (-n) . (+ 6n) =
e) (-6x²) . (+3x²) =
f) (-2y) . (5y) =
g) (+4x²) . (+5x³) =
h) (2y) . (-7x) =
i) (-2x) . (-3y) =
j) (+3x) . (-5y) =
k) (-3xy) . (-2x) =
👉Calcule os quocientes:
DIVISÃO
A divisão de dois monômios, basta dividirmos o coeficiente com coeficiente e parte literal com parte literal. E quanto dividimos as partes literais devemos usar a propriedade da potencia que diz para conservar a base e subtrair os expoentes.
a) (15x⁶) : (3x²) =
b) (16x⁴) : (8x) =
c) (-30x⁵) : (+3x³) =
d) (+8x⁶) : (-2x⁴) =
e) (-10y⁵) : (-2y) =
f) (-35x⁷) : ( +5x³) =
g) (+15x⁸) : (-3x²) =
h) (-8x) : (-8x ) =
i) (-14x³) : (+2x²) =
j) (-10x³y) : (+5x²) =
k) (+6x²y) : (-2xy) =
l) (-7abc) : (-ab) =
A divisão de dois monômios, basta dividirmos o coeficiente com coeficiente e parte literal com parte literal. E quanto dividimos as partes literais devemos usar a propriedade da potencia que diz para conservar a base e subtrair os expoentes.
a) (15x⁶) : (3x²) =
b) (16x⁴) : (8x) =
c) (-30x⁵) : (+3x³) =
d) (+8x⁶) : (-2x⁴) =
e) (-10y⁵) : (-2y) =
f) (-35x⁷) : ( +5x³) =
g) (+15x⁸) : (-3x²) =
h) (-8x) : (-8x ) =
i) (-14x³) : (+2x²) =
j) (-10x³y) : (+5x²) =
k) (+6x²y) : (-2xy) =
l) (-7abc) : (-ab) =
BONS ESTUDOS!!
ENTREGAR A ATIVIDADE ATÉ 21/06/2020.


Nenhum comentário:
Postar um comentário